Domain = all positive real numbers;
Range = all positive real numbers
1) As we can see the function below:

since a >0 and b>1 then we can tell that the Domain, i.e. the set of entries of that function can be defined as All positive Real numbers. The definition of a positive number is to be greater than 0.
2) As for the Range, given that a has to be greater than 0 and b greater than 1 this describes an increasing exponential model, like for instance:
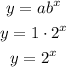
So, any exponential model with these characteristics would have a Range greater than 0 as well: f(x) > 0
3) Thus, the answer is:
Domain = all positive real numbers; range = all positive real numbers