Given:
Find-: Probability that a randomly selected person was either female or was wearing brown shoes.
Sol:
The probability that the randomly selected person was female.
Total female :
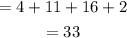
Total = male +female
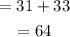
Probability:
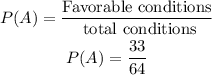
The probability that a randomly selected person was wearing brown shoes.
Total brown shoes:

Total shoes:
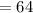
Probability :
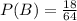
The probability that a randomly selected person was either female or was wearing brown shoes.
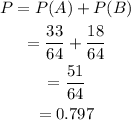
So the probabili