Question

Helio's account has an annual interest rate of 3.3% compounded daily.What is the annual percentage yield for Helio's account?

Answer 1

Let the initial amount be $1 and use the rule of the compounded interest

`A=P(1+(r)/(n))^(nt)`

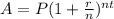
P = 1

r = 3.3% = 3.3/100 = 0.03

n = 365

t = 1

`\begin{gathered} A=1(1+(0.033)/(365))^(365*1) \\ A=1.033548998 \end{gathered}`

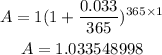
Now find the annual rate using the percent of the increasing rule

`P=(N-O)/(N)*100`

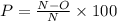
N is the new amount

O is the old amount

`\begin{gathered} \text{Perc}\mathrm{}=(1.033548998-1)/(1)*100 \\ \text{Perc}\mathrm{}=3.355 \end{gathered}`

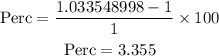
The annual percent is 3.355%