Let the initial amount be $1 and use the rule of the compounded interest
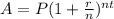
P = 1
r = 3.3% = 3.3/100 = 0.03
n = 365
t = 1
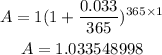
Now find the annual rate using the percent of the increasing rule
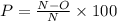
N is the new amount
O is the old amount
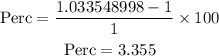
The annual percent is 3.355%