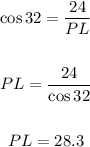Question

Question 7 (4 points)In the figure below, P is the incenter of the AJKL. Determine each of the following measures. Round answers to the tenths place if necessary.MK1335°اما30PON3224LmzOLP=PO =mzPKM =PL=

Answer 1

The answers are :

EXPLANATION :

From the problem, P is the incenter of triangle JKL

Then, PJ, PK and PL are the angle bisectors of angle J, angle K, and angle L.

It means that it divides the angle into two equal measurements.

Solving for angle OLP :

Since PL divides angle L into two equal measurements, angle PLN will be equal to angle OLP

`\begin{gathered} m\angle OLP=m\angle PLN \\ m\angle OLP=32^(\circ) \end{gathered}`

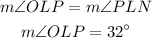
Solving for angle PKM :

From the illustration above, we need to get first the measurement of angle K.

angle L is 32 + 32 = 64

angle J is 35 + 35 = 70

Note that the sum of interior angles in a triangle is 180 degrees.

Then :

`\begin{gathered} m\angle J+m\angle K+m\angle L=180 \\ 70+m\angle K+64=180 \\ m\angle K=180-70-64=46^(\circ) \end{gathered}`

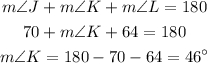
Since PK divides the angle K into two equal measurements, the angle PKM will be half of angle K.

`\begin{gathered} m\angle PKM=(1)/(2)(m\angle K) \\ \\ =(1)/(2)(46) \\ \\ m\angle PKM=23^(\circ) \end{gathered}`

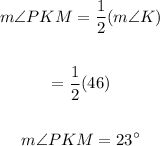
Solving for PO :

We will focus on the triangle OPL

Note that PO is perpendicular to side JL, so angle POL is 90 degrees.

Using tangent function :

`\tan\theta=\frac{\text{ opposite}}{\text{ adjacent}}`

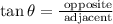
In reference to angle L, the opposite side is PO and the adjacent side is OL = 24

Then :

`\begin{gathered} \tan32=(PO)/(24) \\ \\ PO=24\tan32 \\ PO=14.997\sim15.0 \end{gathered}`

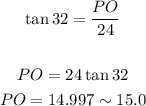
Solving for PL :

Using the same triangle above, the cosine function is :

`\cos\theta=\frac{\text{ adjacent}}{\text{ hypotenuse}}`

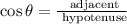
The adjacent side to angle L is OL = 24 and the hypotenuse is PL

Then :

`\begin{gathered} \cos32=(24)/(PL) \\ \\ PL=(24)/(\cos32) \\ \\ PL=28.3 \end{gathered}`