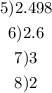
5) In this one, let's take the logarithm on both sides:
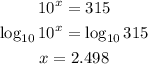
6) Let's begin this exponential equation by simplifying it whenever possible:
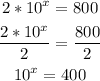
Note that we cannot rewrite 400 as a power of base 10, so let's resort to the logarithm:
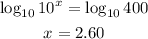
Note that according to the property of the logarithm, we can tell that log_10(10)^x is equal to x
7)
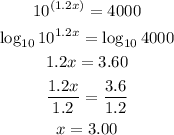
Note that in this case, we had to take the logarithms on both sides right away.
8)
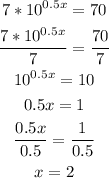
Note that in this case, after dividing both sides by 7 we ended up with two powers of base 10.