Question

On two investments totaling $12,000, Jessica lost 6% on one and earned 7% on the other. If her net annual receipts were $476, how much was each investment?

Answer 1

Given:

The total investment = $12000

Let x denote the first investment anf y denote the second investment.

`x+y=12000\ldots.\ldots(1)`

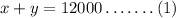
Jessica lost 6% on the first investment and earned 7% on the other.

`\begin{gathered} -6\text{ \%x+7\%y=476} \\ -(6)/(100)x+(7)/(100)y=476 \\ -0.06x+0.07y=476\ldots\text{.}(2) \end{gathered}`

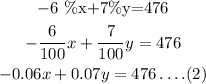
Solve the equations,

`\begin{gathered} x+y=12000 \\ x=12000-y \\ \text{Put it in equation (2)} \\ -0.06(12000-y)+0.07y=476 \end{gathered}`

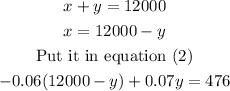
Solving it further,

`\begin{gathered} -0.06(12000-y)+0.07y=476 \\ -720+0.06y+0.07y=476 \\ 0.13y=1196 \\ y=9200 \end{gathered}`

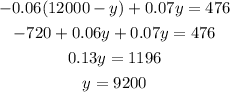
The value of x is,

`\begin{gathered} x=12000-y \\ x=12000-9200 \\ x=2800 \end{gathered}`

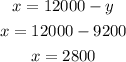
Answer:

The first investment is $2800.

The second investment is $9200.