Given:
The total investment = $12000
Let x denote the first investment anf y denote the second investment.
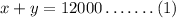
Jessica lost 6% on the first investment and earned 7% on the other.
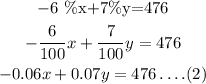
Solve the equations,
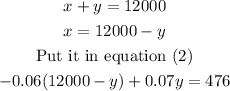
Solving it further,
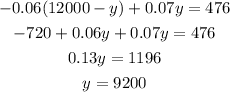
The value of x is,
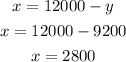
Answer:
The first investment is $2800.
The second investment is $9200.