The helium inside the balloon goes through two states. The first state corresponds to a volume of 744 mL and one atmosphere of pressure. The second state corresponds to 0.5 atm with an unknown volume.
They tell us that the temperature remains constant. We will assume two things:
1. The gas behaves like an ideal gas
2. The ball has no input or output of matter, so the moles remain constant.
When the pressure and volume change at constant moles and temperature of an ideal gas we can apply Boyle's law which tells us:
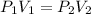
Where,
P1 is the initial pressure of the gas, 1atm
V1 is the initial volume of the gas, 744mL
P2 is the final pressure of the gas, 0.5atm
V2 is the final volume of the gas, unknown.
Now, we clear V2 and replace the known data:
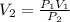
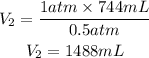
Answer: The gas occupies, at this height, a volume equal to 1488mL