Question

A cube is filled up `10\ in^{3}` of water.If it is dilated by a scale factor of 12, how much water can the dilated cube be able to hold, in `in^{3}`?

Answer 1

The volume of a cube with side L is given by the equation:

`V=L^3`

If the side of a cube is dilated by a scale factor k, its new volume V' will be:

`\begin{gathered} V^(\prime)=(kL)^3=k^3L^3=k^3\cdot V \\ \therefore V^(\prime)=k^3V \end{gathered}`

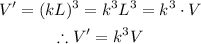
Then, the volume of the cube scaled up by 12, will be:

`\begin{gathered} V=12^3*10in^3 \\ =1,728*10in^3 \\ =17,280in^3 \end{gathered}`

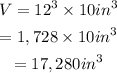
Therefore, the dilated cube will be able to hold 17,280 cubic inches of water.