Question

Consider two planets of mass m and 2m,respectively, orbiting the same star in circularorbits. The more massive planet is 4.5 timesas far from the star as the less massive one.What is the ratio T1 : T2 of the orbital periodsof the two planets?

Answer 1

Given,

The mass of the 1st planet is m

The mass of the 2nd planet is 2m

Let the distance of the lighter planet from its star be r.

Then the distance of the massive planet from the star is 4.5r

Let us assume that the mass of the star is M.

The ratio of the orbital velocity of the two planets is given by,

`\begin{gathered} (v_1)/(v_2)=\frac{\sqrt[]{(GM)/(r)}}{\sqrt[]{(GM)/(4.5r)}} \\ =\sqrt[]{4.5} \end{gathered}`

Where v₁ is the orbital velocity of the 1st planet, v₂ is the orbital velocity of the 2nd planet, and G is the gravitational constant.

The ratio of the orbital period of the two planets is given by,

`\begin{gathered} (T_1)/(T_2)=((2\pi r)/(v_1))/((2\pi*4.5r)/(v_2)) \\ =(1)/((v_1)/(v_2)*4.5) \end{gathered}`

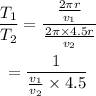
Where T₁ is the orbital period of the 1st planet and T₂ is the orbital period of the 2nd planet.

On substituting the ratio of the orbital velocity,

`\begin{gathered} (T_1)/(T_2)=\frac{1}{\sqrt[]{4.5}*4.5} \\ =\frac{1}{(\sqrt[]{4.5})^3} \end{gathered}`

Therefore the ratio of the orbital periods is T₁:T₂