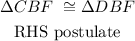Question

Is it possible to prove that triangle CBF is congruent to Triangle DBF

Answer 1

We will investigate the congruency of the composite triangle BCD.

We are given that:

The line common to both the composite triangles is:

`BF\text{ is common}`

Using the application of Pythagorean theorem we have:

`\begin{gathered} BC^2=CF^2+BF^2 \\ BD^2=FD^2+BF^2 \\ CF\text{ = FD} \\ =============== \\ BC^2=BD^2 \\ =============== \\ BC\cong BD \end{gathered}`

Hence, using the congruency postulate for right angled triangles we have:

`\begin{gathered} \Delta CBF\text{ }\cong\Delta DBF \\ \text{RHS postulate} \end{gathered}`