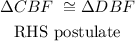We will investigate the congruency of the composite triangle BCD.
We are given that:
![<\text{CBF }\congUsing the sketch avaliable we can make the following statements:[tex]BF\text{ is a bisector of CD , imply If the point ( F ) is the midpoint of the line segment CD then we can say:[tex]CF\text{ }\cong FD]()
The line common to both the composite triangles is:
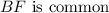
Using the application of Pythagorean theorem we have:
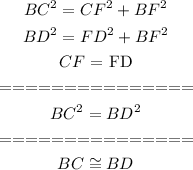
Hence, using the congruency postulate for right angled triangles we have: