Question

I am doing this exercise and then I have a few questions like this one and I am very confused on how to do this I really could use some help if you can help me with this one then I can do the other exercises I don’t know where to start I really need help step by step been 20 year since I’ve done math please help thank you I’m trying to do these exercises to educate myself in mathematics and prepare myself for a GED thst I will take when I’m ready

Answer 1

a)

The table shows the values of the function P(X) for every value of X from 0 to 10; then, as suggested by the question, to determine the probability that at least 5 users have abandoned their landlines, add P(5) to P(10), as shown below

`P(X\ge5)=P(5)+P(6)+...+P(10)=0.2087+0.1209+...+0.01=0.402`

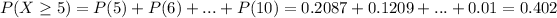
Thus, the answer to part a) is 0.402.

Alternatively,

`\begin{gathered} P(X\ge5)=1-P(X<5)=1-(P(0)+P(1)+P(2)+P(3)+P(4)) \\ =1-(0.6078) \\ =0.3922 \end{gathered}`

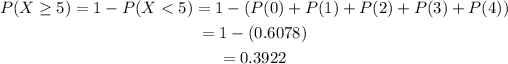
There is a difference between both results because the data in the table add up to 1.0098, not 1 as it should be.

b)

The binomial distribution states that

`\begin{gathered} P(X=k)=(nbinomialk)p^k(1-p)^(n-k) \\ where \\ (nbinomialk)=(n!)/((n-k)!k!),n!=1*2*3*...*n \\ n\rightarrow\text{ total number of trials} \\ k\rightarrow\text{ number of successful trials} \\ p\rightarrow\text{ probability of a successful trial} \end{gathered}`

In our case, consider that a successful trial consists of a user abandoning their landline; thus,

`\begin{gathered} n=10,k=5,p=44\%=(44)/(100)=0.44 \\ \end{gathered}`

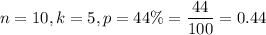
Thus, the corresponding probability is

`\begin{gathered} P(X=5)=(10binomial5)(0.44)^5(1-0.44)^(10-5)=(10!)/(5!5!)(0.44)^5(0.56)^5 \\ =252(0.44)^5(0.56)^5 \\ \approx0.228878... \end{gathered}`

The approximate answer is 0.228878...