Question

What is the area of the given triangle? Round to thenearest tenth

Answer 1

Consider that the given diagram is a triangle ABC with base BC 13cm, side AC 7cm, and an included angle of 38 degrees.

Consider the following diagram,

Construction: Draw a perpendicular from A to BC at point M, such that AM represents the height of the triangle ABC.

Apply the sine ratio in the triangle AMC,

`\begin{gathered} \sin \theta=\frac{\text{ Opposite Side}}{\text{ Hypotenuse}} \\ \sin 38^(\circ)=(AM)/(AC) \\ 0.61566=(AM)/(7) \\ AM=0.61566*7 \\ AM\approx4.31 \end{gathered}`

Now, the area of the triangle is calculated as,

`\begin{gathered} Area=(1)/(2)* BC* AM \\ Area=(1)/(2)*13*4.31 \\ Area\approx28.0 \end{gathered}`

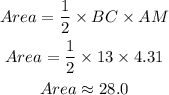
Thus, the area of the given triangle is 28.0 square centimeters.