Question

Write a new equation for the circle (x-3)^2 + (y+8)^2 =25 after it is shifted left 5 units and up 2 units.

Answer 1

Step 1: Write out the formula

Given the equation of a circle with center (h,k) and radius r, if it is shifted left by a unit and up by b unit, then the function would become

`(x-h+a)^2+(y-k-b)^2=r^2`

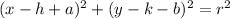
Step 2: Write out the given value and substitute them into the formula

In this case,

`h=3,k=-8,a=5,b=2,r=5`

Therefore the new equation is given by

`\begin{gathered} (x-3+5)^2+(y-(-8)-2)^2=5^2 \\ (x+2)^2+(y+8-2)^2=5^2 \\ (x+2)^2+(y+6)^2=25 \end{gathered}`

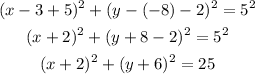
Hence, the new equation for the circle is (x+2)²+(y+6)²=25