Question

A red car & blue car travel at the same speed. The

red car drives 4 hours. The blue car goes another
half hour and goes 40 miles. A yellow car
leaves 15 minutes after the red car but travels
12 mph faster. How long bed does the yellow car
drive before passing the red car? Solve with equation.

Answer 1

So we have a red and a blue car moving at the same speed x. The red car goes for 4 hours and the blue car for 4.5 hours. The distance they traveled is given by the product of their speed and the time they were moving:

`\begin{gathered} 4x \\ 4.5x \end{gathered}`

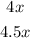
If the blue car went for 40 more miles than the red car then the distance traveled by the blue car is that of the red car plus 40:

`4.5x=4x+40`

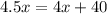
This equation gives us the speed of both cars. We can substract 4x from both sides:

`\begin{gathered} 4.5x-4x=4x-4x+40 \\ 0.5x=40 \end{gathered}`

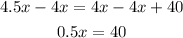
And we divide both sides by 0.5:

`\begin{gathered} (0.5x)/(0.5)=(40)/(0.5) \\ x=80 \end{gathered}`

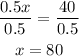
So the red and blue cars travel at 80 mph. This means that the yellow car travels at 80 mph + 12 mph=92 mph. So now we have to find the time at which the yellow car travelling at 92 mph passes the red car traveling at 80 mph. The distance travelled by the red car in miles t minutes after it started to move is:

`80t`

The distance traveled by the yellow car in miles t minutes after the red car started to move is:

`92\cdot(t-15)`

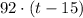
That -15 takes into account that the yellow car only started moving 15 minutes after the red one. It is also important to note that this equation is only valid after t=15. The yellow car reaches the red car at the time where their distances are equal. The equation that gives us this time is then:

`\begin{gathered} 80t=92\cdot(t-15) \\ 80t=92t-1380 \end{gathered}`

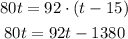
We add 1380 to both sides and substract 80t from both:

`\begin{gathered} 80t+1380-80t=92t-1380-80t \\ 1380=12t \end{gathered}`

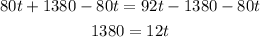
Then we divide both sides by 12:

`\begin{gathered} (1380)/(12)=(12t)/(12) \\ 115=t \end{gathered}`

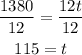
So they met 115 minutes after the red car started moving. We have to tell how long does the yellow car drive before passing the red so if the red car was driving for 115 minutes the yellow car was driving for:

`115-15=100`

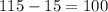
100 minutes. For the distance the yellow car traveled we need to expressed those minutes in hours so we have to divide them by 60. Then the distance traveled by the yellow car is:

`92\cdot(100)/(60)=153.33`

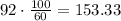
So the yellow car drove for 100 minutes and 153.33 miles before passing the red car.