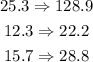
Step-by-step explanation
to solve this we need to use the law of cosine
it says,
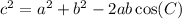
then
Step 1
let
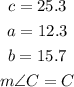
replace

images
128.9 °
Step 2
angle across the side 12.3
exacty as the previous step , we just need to reorder, so

Step 3
finally, the angle across the side 15.7

I hope this helps you