To answer this question, we need to take into account that we have here operations with mixed fractions. Then, we can pose the operations as follows:
1. We have a total of 68 and 3/4 acres.
2. How many acres of wooded land will remain if we subtract 4/5 acres from the total?
Then, we can proceed as follows:
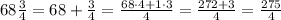
Thus, we have that 4/5 from the total is:

We have that 55 acres are cleared for development. We have at the beginning 275/4 acres (68 plus 3/4 acres). Now, we need to subtract 55 acres from the latter. Then, we have:
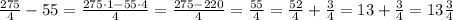
Therefore, there will remain 13 and 3/4 of acres of wooded land (first option).
(As we can see this last value is 1/5 of the total acres of the wooded piece of land.)