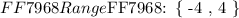Domain are a set of values of ( x ) which serves as an input to the function. The set of values of ( x ) qualifies the domain over which the function f ( x ) is defined over.
Function f ( x ) is a relationship between the input and output. It is expressed as an mathematical expression of any form.
The following set of values given to us:
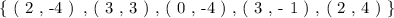
The pair of values are expressed as follows:
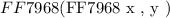
Where,
![\begin{gathered} x\colon\text{ Domain ( input )} \\ y\text{ : Function ( output ) - f ( x )} \end{gathered}]()
The domain is a set of values of ( x ) from lowest to highest as follows:

Hence, we can write the domain as follows:

Similarly we can express the range of values for the output by considering the highest and lowest output.
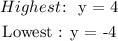
Hence, we can write the domain as follows: