Question

for the following set of numbers, find the mean, median, mode and midrange.10, 10, 11, 12, 14, 14, 15, 26

Answer 1

Given the set of values

10, 10, 11, 12, 14, 14, 15, 26

You have to calculate the measures of center position, mean, median, and mode:

Mean

To determine the mean you have to add all number of the set and divide it by the number of values:

`\begin{gathered} \text{Mean}=(\Sigma x)/(n) \\ \end{gathered}`

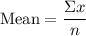
There are n=8 values on this set, then you can calculate the mean as follows:

`\begin{gathered} \text{Mean}=(10+10+11+12+14+14+15+26)/(8) \\ \text{Mean}=(112)/(8) \\ \text{Mean}=14 \end{gathered}`

The mean value of the set of numbers is 14.

Median

The median of a set of values is the number that divides the set in two, to determine which value corresponds to the median you have to calculate its position.

The position of the median for an even set of numbers can be calculated as follows:

`\text{PosMe}=(1)/(2)n`

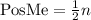
For this set the position of the median is:

`\begin{gathered} \text{PosMe}=(1)/(2)\cdot8 \\ \text{PosMe}=4 \end{gathered}`

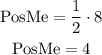
The median is the fourth value of the set.

To identify which value is the median, all observations of the set must be arranged from least to greatest, then, you can determine the median:

10, 10, 11, 12, 14, 14, 15, 26​

The fourth value of the set is 12, which means that the median of the set is 12.

Mode

The mode of a set of values is the value/s that are most observed, which means, it's the most repeated value.

For this set, there are two values that are repeated two times, 10 and 14.

So this set of numbers has two modes:

Mode 1 = 10

Mode 2 = 14