Question

Solve.2^x-3 = (1/2)^2x-3Answer additional questions in the Show Your Work space.What is the first step to solving the equation?

Answer 1

x = 2

First step: Apply logarithm in both sides

Step-by-step explanation:

The given expression is

`2^(x-3)=((1)/(2))^(2x-3)`

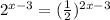
Then, the first step is to apply logarithm in base 2 to both sides, so

`\begin{gathered} \log _22^(x-3)=\log _2((1)/(2))^(2x-3)_{^{}} \\ (x-3)\log _22=(2x-3)\log _2((1)/(2)) \end{gathered}`

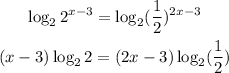
Then, we can calculate the logarithms and solve for x, so

`\begin{gathered} (x-3)(1)=(2x-3)(-1) \\ x-3=2x(-1)-3(-1) \\ x-3=-2x+3 \end{gathered}`
`\begin{gathered} x-3+3=-2x+3+3 \\ x=-2x+6 \\ x+2x=-2x+6+2x \\ 3x=6 \\ (3x)/(3)=(6)/(3) \\ x=2 \end{gathered}`

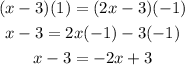
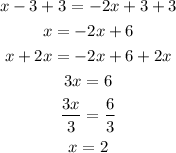
Therefore, the solution is x = 2