Answer:
x = 2
First step: Apply logarithm in both sides
Step-by-step explanation:
The given expression is
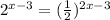
Then, the first step is to apply logarithm in base 2 to both sides, so
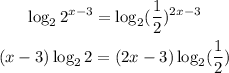
Then, we can calculate the logarithms and solve for x, so

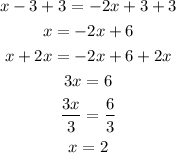
Therefore, the solution is x = 2