The graph of the constant function y = c is a horizontal line in the plane that passes through the point (0, c).
In the context of a polynomial in one variable x, the non-zero constant function is a polynomial of degree 0 and its general form is f(x) = c where c is nonzero. This function has no intersection point with the x-axis, that is, it has no root (zero). On the other hand, the polynomial f(x) = 0 is the identically zero function. It is the (trivial) constant function and every x is a root. Its graph is the x-axis in the plane.
The graph below is a constant graph function at
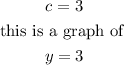
This means that the y-intercept is
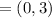
The general equation of a line is given as
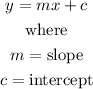
Since its a constant graph, that means the graph has the repeated domain for the same value of the range at y =2
Therefore,
the coordinates of the line will be
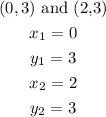
The formula us to calculate the slope of the line is given below as
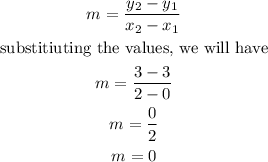
Therefore,
The line in the graph has a ZERO SLOPE
The Final answer is OPTION C