Question

Graph the linear equation y= -5x + 2. on graph paper

Answer 1

Given the Linear Equation:

`y=-5x+2`

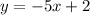
You can find the y-intercept and the x-intercept in order to graph it.

Notice that it is written in Slope-Intercept Form:

`y=mx+b`

Where "m" is the slope of the line and "b" is the y-intercept.

In this case, you can identify that the y-intercept is:

`b=2`

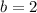
In order to find the x-intercept, you need to substitute this value of "y" into the equation:

`y=0`

Because the value of "y" is zero when the line intersects the x-axis.

Then, substituting that value and solving for "x", you get:

`\begin{gathered} y=-5x+2 \\ 0=-5x+2 \\ -2=-5x \\ \\ (-2)/(-5)=x \\ \\ x=0.4 \end{gathered}`

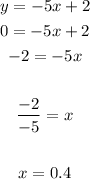
Now that you know that the line passes through these points:

`(0.4,0),(0,2)`

You can plot them on the Coordinate Plane. See the picture below:

Finally, draw the line passing through those points.

Hence. the answer is: