Question

How many ounces of a 12 % alcohol solution and a 20 % alcohol solution must be combined to obtain 48 ounces of a 16% solution?

Answer 1

24 oz of 12% alcohol and 24oz of 20% alcohol

1) We can solve this problem, writing out a Linear Equation System. So we can write out the following, calling alcohol 12% x, and y an 20% alcohol solution

`\begin{gathered} x+y=48 \\ 12x+20y=16(48) \end{gathered}`

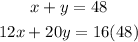
2) So, based on that, the first equation refers to the weight, and the second one to the quantities of each we can write out:

`\mleft\{\begin{matrix}x+y=48 & \\ 12x+20y=768 & \end{matrix}\mright.`

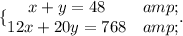
Let's use the Addition/Elimination Method

`\begin{gathered} \mleft\{\begin{matrix}x+y=48*(-12) & \\ 12x+20y=768 & \end{matrix}\mright. \\ \mleft\{\begin{matrix}-12x-12y=-576 & \\ 12x+20y=768 & \end{matrix}\mright. \\ ---------------- \\ 8y=192 \\ (8y)/(8)=(192)/(8) \\ y=24 \end{gathered}`

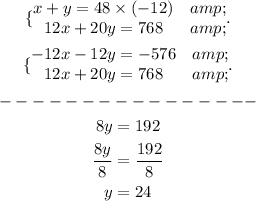
So we need 24 ounces for the 20% Alcohol solution, let's finally find the quantity for the 12% Alcohol:

`\begin{gathered} x+24=48 \\ x=48-24 \\ x=24 \end{gathered}`

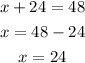
3) Hence, the answer is 24 oz of 12% alcohol and 24oz of 20% alcohol