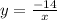SOLUTION
If the table represents an inverse variation, it means that y is inversely proportional to x, written as
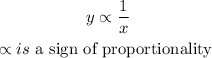
Removing the proportionality sign and introducing a constant k, we have
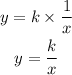
In the first column, we have x = -4 and y = 3.5. Substituting these values for x and y, we have
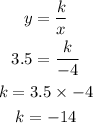
So, if it's an inverse variation, the relationship would be
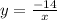
In the second column, x = -2 and y = 7.
Now lets substitute the value of x for -2. If we get y to be 7, then the relationship is an inverse variation
We have
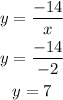
Since we got y = 7, the relationship is therefore an inverse variation.
The constant k = -14
The equation for the inverse variation is