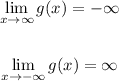Question

What are lim x→∞ g(x) and lim x→−∞g(x)? Briefly explain your answer.

Answer 1

Given the function:

`g(x)=-3x^5+2x^4-5x^2+8`

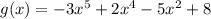
Let's find the limit of the function as x approaches infinity and also as x approaches negative infinity.

We have:

`\begin{gathered} \lim _(x\to\infty)-3x^5+2x^4-5x^2+8 \\ \\ \lim _(x\to\infty)g(x)=-\infty \end{gathered}`

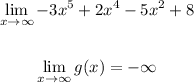
The limit at infinity of a polynomial whose leading coefficient is negative is negative infinity.

• Also, the limit of the function at negative infinity:

`\begin{gathered} g(x)=-3x^5+2x^4-5x^2+8 \\ \\ \lim _(x\to-\infty)g(x)=\infty \end{gathered}`

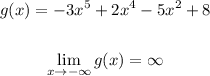
The limit at negtaive infinity of a polynomial whose leading coefficient is negative is infinity.

ANSWER:

`\begin{gathered} \lim _(x\to\infty)g(x)=-\infty \\ \\ \lim _(x\to-\infty)g(x)=\infty \end{gathered}`