Question

Solving a percent mixture problem using asystem of linear equations

Answer 1

Let x be the number of pints of 65% pure fruit juice drink and y the number of pints of the 90% pure fruit juice drink

Then we have:

`\begin{gathered} x+y=90 \\ (0.65x+0.9y)/(90)=0.7 \end{gathered}`

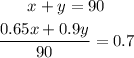
From the first equation, we have y = 90 - x.

Replacing y in the second equation, we got:

`\begin{gathered} (0.65x+0.9(90-x))/(90)=0.7 \\ 0.65x+0.9(90-x)=63 \\ 0.65x+81-0.9x=63 \\ 0.25x=18 \\ x=72 \\ \therefore y=90-72=18 \end{gathered}`

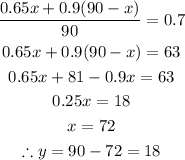
Answer:

First fruit drink: 72 pints

Second fruit drink: 18 pints