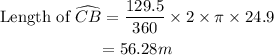Answer:
• 259 degrees
,
• 112.56m
,
• 56.28m
Step-by-step explanation:
In the circle:
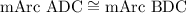
The sum of the angle in a circle = 360 degrees
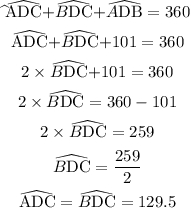
Part 8
The measure of arc ACB.
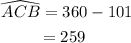
Part 9
Length of arc ACB

Therefore:
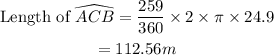
Part 10
Length of arc CB.
The central angle subtended by CB = 129.5 degrees
Therefore: