Let x be the number of 2-point shots
Let y be the number of 1-point shots
The team made 57 successful shots: The sum of x and y is 57:
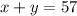
The team scored 94 points in all: 2 times x and y sum 94:
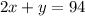
System of equations:
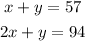
Use elimination method to solve the system of equations:
1. Subtract the equations:
2. Solve x:
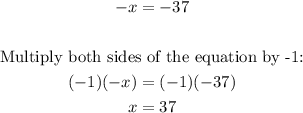
3. Use the value of x to solve y:
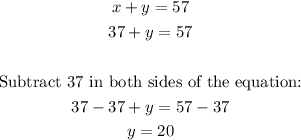
Solution for the system x=37 and y=20
Then, there were 37 2-point shots and 20 1-point shots