Question

At a basketball game, a team made 57 successful shots. They were a combination of 1- and 2-pointshots. The team scored 94 points in all. Write and solve a system of equations to find the number ofeach type of shot.There were2-point shots and1-point shots

Answer 1

Let x be the number of 2-point shots

Let y be the number of 1-point shots

The team made 57 successful shots: The sum of x and y is 57:

`x+y=57`

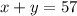
The team scored 94 points in all: 2 times x and y sum 94:

`2x+y=94`

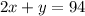
System of equations:

`\begin{gathered} x+y=57 \\ 2x+y=94 \end{gathered}`

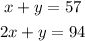
Use elimination method to solve the system of equations:

1. Subtract the equations:

2. Solve x:

`\begin{gathered} -x=-37 \\ \\ \text{Multiply both sides of the equation by -1:} \\ (-1)(-x)=(-1)(-37) \\ x=37 \end{gathered}`

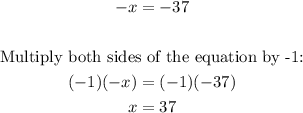
3. Use the value of x to solve y:

`\begin{gathered} x+y=57 \\ 37+y=57 \\ \\ \text{Subtract 37 in both sides of the equation:} \\ 37-37+y=57-37 \\ y=20 \end{gathered}`

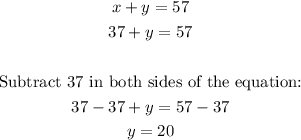
Solution for the system x=37 and y=20

Then, there were 37 2-point shots and 20 1-point shots