Given:
Two pipes can fill a tank in 60 min
If only one is used, it would take 23 min longer for the smaller pipe
Let the time it takes for the smaller pipe to fill the tank be x
The time it would take the larger pipe would be:
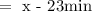
Since the two pipes can fill the tank in 60 min.
The rate at which the smaller pipe plus the rate which the larger pipe fills the tank would be equal to 1:
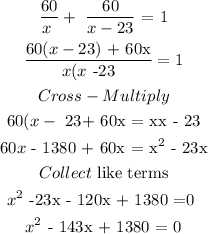
Next, we solve the quadratic equation:
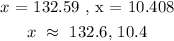
Hence, the time it takes for the smaller pipe is 132.6 min