Question

Two pipes can fill a tank in 60 minutes if both are turned on. If only one is used, it would take 23 minutes longer for the smaller pipe tofill the tank than the larger pipe. How long will it take for the smaller pipe to fill the tank? (Round your answer to the nearest tenth.)AnswerKeypad

Answer 1

Given:

Two pipes can fill a tank in 60 min

If only one is used, it would take 23 min longer for the smaller pipe

Let the time it takes for the smaller pipe to fill the tank be x

The time it would take the larger pipe would be:

`=\text{ \lparen x - 23\rparen min}`

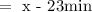
Since the two pipes can fill the tank in 60 min.

The rate at which the smaller pipe plus the rate which the larger pipe fills the tank would be equal to 1:

`\begin{gathered} \frac{60}{x\text{ }}+\text{ }(60)/(x-23)\text{ = 1} \\ \frac{60(x-23)\text{ + 60x}}{x(x\text{ -23\rparen}}=1 \\ Cross-Multiply \\ 60(x-\text{ 23\rparen + 60x = x\lparen x - 23\rparen} \\ 60x\text{ - 1380 + 60x = x}^2\text{ - 23x} \\ Collect\text{ like terms} \\ x^2\text{ -23x - 120x + 1380 =0 } \\ x^2\text{ - 143x + 1380 = 0} \end{gathered}`

Next, we solve the quadratic equation:

`\begin{gathered} x\text{ = 132.59 , x = 10.408} \\ x\text{ }\approx\text{ 132.6, 10.4} \end{gathered}`

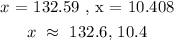
Hence, the time it takes for the smaller pipe is 132.6 min