Range of the Exponential Function
The range of a function y = f(x) is the set of all the functions' values when x moves through its domain.
It's required to find the range of the function:
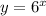
The domain of the function is the set of all the real numbers because x can be given any possible value and y would still exist.
For example, let's give x the values x={-3,-1,0,2,4}
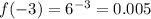
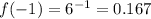
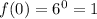
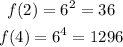
It's clear that for negative values of x, the function tends to zero and for positive values, the function tends to infinity.
Thus, the range of the function is (0,