Question

How do I do number 5 part a and b?

Answer 1

Given:

There are 10 smartphones.

Out of 10, there are 7 good and 3 defective smartphones.

Step-by-step explanation:

a) To find: The number of ways exactly 4 good smartphones are selected when buying 5 smartphones

The number of ways is,

`\begin{gathered} ^7C_4*^3C_1=(7!)/((7-4)!4!)*(3!)/((3-1)!1!) \\ =(7!)/(3!4!)*(3!)/(2!1!) \\ =(5*6*7)/(3*2*1)*3 \\ =5*7*3 \\ =105\text{ ways} \end{gathered}`

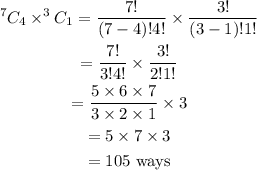
b) To find: The number of ways atleast 3 good smartphones are selected when buying 5 smartphones

The number of ways is,

`\begin{gathered} ^7C_3*^3C_2+^7C_4*^3C_1+^7C_5=(7!)/((7-3)!3!)*(3!)/((3-2)!2!)+(7!)/((7-4)!4!)*(3!)/((3-1)!1!)+(7!)/((7-5)!5!)\frac{}{1!} \\ =(7!)/(4!3!)*(3!)/(1!2!)+(7!)/(3!4!)*(3!)/(2!1!)+(7!)/(2!5!) \\ =(5*6*7)/(3*2*1)*3+(5*6*7)/(3*2*1)*3+(6*7)/(1*2) \\ =5*7*3+5*7*3+3*7 \\ =105+105+21 \\ =231\text{ ways} \end{gathered}`

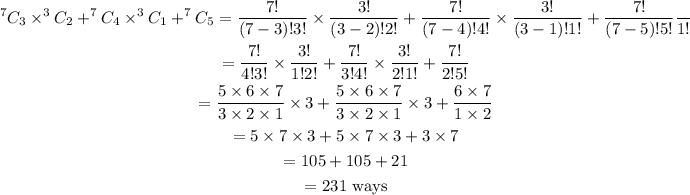
Final answer:

a) 105 ways

b) 231 ways