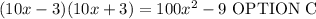Solution
- The question would like us to expand the brackets in the expression below:
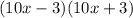
- We can proceed to expand this normally, but instead of going through the tedious process of doing that, we can simply observe that this question is a scenario of a "Difference of two squares". "Difference of two squares" is defined below:
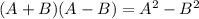
- In this case, we can think of it like this:
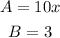
- Thus, we can easily expand this expression as follows:
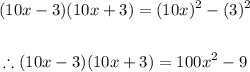
Final Answer
The answer is