1. Find the vector between each pair of vertices:
To make it more easy give to each vertex a letter:
A(1,3)
B(3,5)
C(2,6)
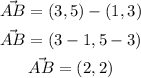
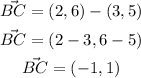
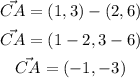
2. Find the magnitude of each vector:
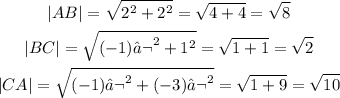
3. Fid the dot product beween each pair of vectors:
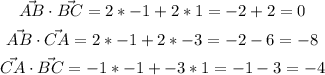
4. Use the next formula to find the angle betweeen two vectors:
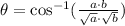
Angle between AB and BC:
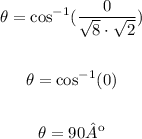
Angle between AB and CA:
