We have to find the other endpoint of the line segment with:
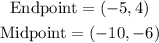
For doing so, we will have to find the x and y-coordinates of the point.
First, we will find the line for which the two points pass through. Then, we will find the x-coordinate of the endpoint, using the definition of midpoint, and finally, we will use the x-coordinate and the function for finding the y-coordinate of the point.
Finding the line
We will find the slope, and the y-intercept. For the slope, we use the formula:
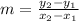
where (x₁,y₁) and (x₂,y₂) are the coordinates of the points. Using it we find:
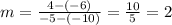
This means that the slope is 2. Now, for the y-intercept, we replace on the general slope-intercept formula:

And we get that:

We get that the equation of the line is:
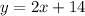
Finding the x-coordinate
For this step, we know that the distance in the x-coordinates between the midpoint and the endpoint is:
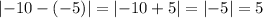
This means that the distance in the x-coordinates between the midpoint and the other endpoint is also 5. Thus, as it is moving to the left, the x-coordinate will be -10-5=-15.
Finding the y-coordinate
For this step, we replace the x-coordinate onto the function obtained on the step 1, and we will get the y-coordinate of the other endpoint.