Question

What is the radius of a sphere with a volume of 47270 cm 3, to the nearest tenth of a centimeter.

Answer 1

22.4cm

Volume of a Sphere :

V = 4/3πr3

47270 = (4/3π)r3

47270/4.18 = 4.18r3/4.18

11284.8812399 = r3

Cube root that then your answer should be 22.4cm.

Answer 2

Given:

The volume of the sphere is 47270 cm³.

To find- the radius of the sphere.

Explanation-

We know that the formula of the volume of the sphere is given by-

`volume=(4)/(3)\pi r^3`

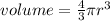
where r is the radius of the sphere.

Substitute the values to get r, and we get

`47270=(4)/(3)*(22)/(7)* r^3`

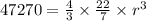
Transpose the equation, and we get

`\begin{gathered} r^3=47270*(3)/(4)*(7)/(22) \\ r^3=23635*(3)/(2)*(7)/(22) \end{gathered}`

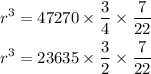
On further solving, we get

`\begin{gathered} r^3=(496335)/(44) \\ r^3=11280.34091 \\ r=\sqrt[3]{11280.34091} \\ r=22.4271 \end{gathered}`

Thus, the radius of the sphere is 224271 cm.

And on rounding it off to the nearest tenth of a centimeter, the radius of the sphere becomes 22.4cm.

The answer is 22.4cm.