Given:
The volume of the sphere is 47270 cm³.
To find- the radius of the sphere.
Explanation-
We know that the formula of the volume of the sphere is given by-
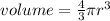
where r is the radius of the sphere.
Substitute the values to get r, and we get
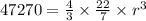
Transpose the equation, and we get
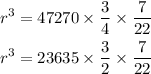
On further solving, we get
![\begin{gathered} r^3=(496335)/(44) \\ r^3=11280.34091 \\ r=\sqrt[3]{11280.34091} \\ r=22.4271 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/1gemnb3ec0zr7ow3y31lzxl3454o4d1kh2.png)
Thus, the radius of the sphere is 224271 cm.
And on rounding it off to the nearest tenth of a centimeter, the radius of the sphere becomes 22.4cm.
The answer is 22.4cm.