Given the following System of equation:
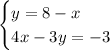
You can solve it using the Substitution method. The steps are shown below:
1. You can substitute the first equation into the second equation:
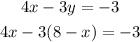
2. Now you have to solve for the variable "x":
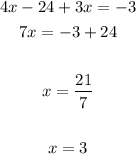
3. Finally, substitute the value of "x" into the first equation and evaluate, in order to find the value of "y". Then:
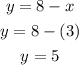
You can write the solution in this form:
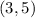
The answer is: Option C.