Question

the school newspaper has a circulation of 500 and sells for $.035 a copy. the students decide to raise the price to increase their income and conduct a survey. they find for every $0.05 they increase the price they will lose 20 subscribers. what price per copy maximizes the income? solve and show work.

Answer 1

Let x be the number of times they raise the price on the newspaper. Then the new cost of the newspaper is

`.35+.05x`

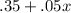
Let y be the newspaper they sell, then the income will be

`y(.35+.05x)`

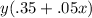
Now, we know that the circulation is of 500, assuming that they sold every newspaper at the original price now the number the will sell will be

`y=500-20x`

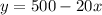
Plugging the value of y in the first expression we have that the income will be

`\begin{gathered} f(x)=(500-20x)(.35+\text{0}.5x)=175+25x-7x-x^2 \\ =-x^2+18x+175 \end{gathered}`

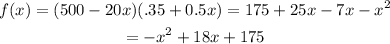
Then the income is given by the function

`f(x)=-x^2+18x+175`

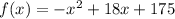
To find the maximum value of this functions (thus the maximum income) we need to take the derivative of the function,

`\begin{gathered} (df)/(dx)=(d)/(dx)(-x^2+18x+175) \\ =-2x+18 \end{gathered}`

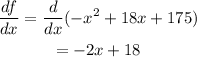
no we equate the derivative to zero and solve for x.

`\begin{gathered} (df)/(dx)=0 \\ -2x+18=0 \\ -2x=-18 \\ x=(-18)/(-2) \\ x=9 \end{gathered}`

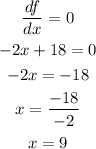
This means that we have an extreme value of the function when x=9. Now we need to find out if this value is a maximum or a minimum. To do this we need to take the second derivative of the function, then

`\begin{gathered} (d^2f)/(dx^2)=(d)/(dx)((df)/(dx)) \\ =(d)/(dx)(-2x+18) \\ =-2 \end{gathered}`

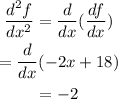
Since the second derivative is negative in the point x=9, we conclude that this value is a maximum of the function.

With this we conclude that the number of times that they should raise the price to maximize the income is 9. This means that they will raise the price of the newspaper (9)($0.05)=$0.45.

Therefore the price to maximize the income is $0.35+$0.45=$0.80.