Question

A crane is being set up on a slope of 3.5°. If the base of the crane is 8.0 ft wide, how many inches should the downhill side of the base be raised in order to level the crane?Round to the nearest TENTH as needed

Answer 1

Lets draw a picture of the problem:

Since we have a right triangle, we can relate the given angle with the sides by means of the tangent function, that is,

`\tan 3.5=(x)/(8)`

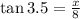
By multiplying both sides by 8, we have

`\begin{gathered} 8\cdot\tan 3.5=x \\ or\text{ equivalently, } \\ x=8\cdot\tan 3.5 \end{gathered}`

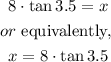
Since tan3.5= 0.06116, we get

`\begin{gathered} x=8*0.06116 \\ x=0.4893\text{ ft} \end{gathered}`

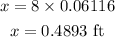
Since 1 feet is equal to 12 inches, we have

`\begin{gathered} 0.4893ft=0.4893ft((12in)/(1ft)) \\ \text{which gives} \\ 0.4893ft=5.87in \end{gathered}`

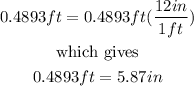
Therefore, by rounding to the nearest tenth, the answer is 5.9 inches.