Lets draw a picture of the problem:
Since we have a right triangle, we can relate the given angle with the sides by means of the tangent function, that is,
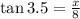
By multiplying both sides by 8, we have

Since tan3.5= 0.06116, we get
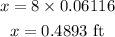
Since 1 feet is equal to 12 inches, we have
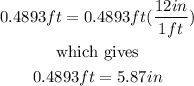
Therefore, by rounding to the nearest tenth, the answer is 5.9 inches.