To get the standard deviation of the probability distribution, we will use the formula below
![\sigma=\sqrt[]{\sum ^{}_{}(x-\bar{x})^2* P(x)}](https://img.qammunity.org/2023/formulas/mathematics/college/hi3f7ml284th7mqdp4p5481hjeemrm3j4a.png)
where
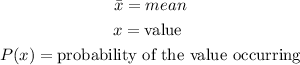
Step 1: To begin with, we will get the mean first
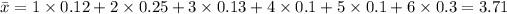
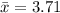
Next, we will find
![\begin{gathered} \sum ^{}_{}(x-\bar{x})^2* p(x)=0.12(1-3.71)^2+0.25(2-3.71)^2+0.13(3-3.71)^2+0.1(4-3.71)^2+0.1(5-3.71)^2+0.3(6-3.71)^2 \\ =3.4259 \end{gathered}]()
The final step will be to find the square root of the value obtained above
![\sqrt[]{\sum ^{}_{}(x-\bar{x})^2* p(x)}=\sqrt[]{3.4259}=1.851](https://img.qammunity.org/2023/formulas/mathematics/college/qlbboqlhsd9ua1074zokszgzj6nhn7vjkk.png)
From the options provided, the closest answer is 1.84
Thus, the answer is 1.84