Question

A fair die is tossed. The following table represents the probability distribution of the experiment.

Answer 1

To get the standard deviation of the probability distribution, we will use the formula below

`\sigma=\sqrt[]{\sum ^{}_{}(x-\bar{x})^2* P(x)}`

where

`\begin{gathered} \bar{x}=mean \\ x=\text{value } \\ P(x)=\text{probability of the value occurring} \end{gathered}`

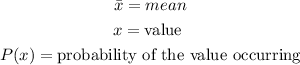
Step 1: To begin with, we will get the mean first

`\bar{x}=1*0.12+2*0.25+3*0.13+4*0.1+5*0.1+6*0.3=3.71`

`\bar{x}=3.71`

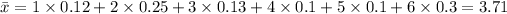
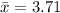
Next, we will find

The final step will be to find the square root of the value obtained above

`\sqrt[]{\sum ^{}_{}(x-\bar{x})^2* p(x)}=\sqrt[]{3.4259}=1.851`

From the options provided, the closest answer is 1.84

Thus, the answer is 1.84