Since the monthly charge S is made from 2 parts,
A constant part, let it b
A part depends on a direct relationship between it and the time t
Then the form of S should be

Where:
m is the rate of change
b is the constant amount
Since S = 230 at t = 100
Since S = 290 at t = 130
Substitute them in the equation above to make 2 equations of m, b and solve them
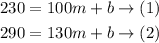
Subtract equation(1) from equation (2) to eliminate b
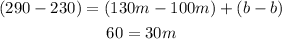
Divide both sides by 30 to find m
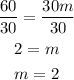
Substitute m in equation (1) by 2 to find b
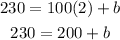
Subtract both sides by 200
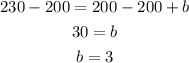
a) The equation of S is (substitute m by 2 and b by 30)

b) Since the monthly fee is $330, then
S = 330
Substitute it in the equation to find t
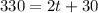
Subtract 30 from both sides
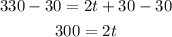
Divide both sides by 2 to find t
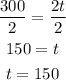
The value of the time is 150 minutes