Question

Two dice dice are rolled, what is probability thatthe sum is 7 or more? Enter your answer as afraction.

Answer 1

7/12

Explanation:

The sample space of throwing two 6-sided dice can be calculated as follows:

`\begin{gathered} s=6^2 \\ \\ s=36 \end{gathered}`

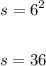
Now, the sample space that the sum of the dice is 7 or more would be the following:

{(1, 6). (2, 5), (2, 6), (3, 4), (3, 5), (3, 6), (4, 3), (4, 4), (4, 5), (4, 6), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}= 21 outcomes

In total there are 21 events where it can happen that the sum is 7 or more, therefore, the probability would be:

`\begin{gathered} p=(21)/(36) \\ \\ p=(7)/(12) \end{gathered}`

The probability is equal to 7/12