Question

I really need help on this can you help me please

Answer 1

When given a quadratic equation and we seek the vertex coordinates, we have to arrange such equation into its vertex form. The vertex form goes thus:

`\begin{gathered} f(x)=a\mleft(x-h\mright)^2+k \\ \text{Vertex is at (h, k)} \end{gathered}`

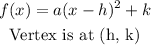
If we put our equation in this form, we get:

`\begin{gathered} f(x)=-2(x+3)^2-1 \\ ReArrangi\text{ng, we get:} \\ f(x)=-2(x-(-3))^2+(-1) \end{gathered}`

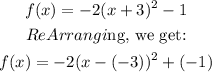
Therefore, our vertex, based on the general form is: (-3 , -1)

The domain of a function is the set into which all of the input of the function is constrained to fall, i.e, all the values of x that validates the function.

The domain is all real numbers

The range of a function is the set of outputs the function achieves when it is applied to its whole set of inputs. The set of the values of f(x) when the domain is applied.

The range is therefore:

`y\le-1`

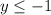
Third Option